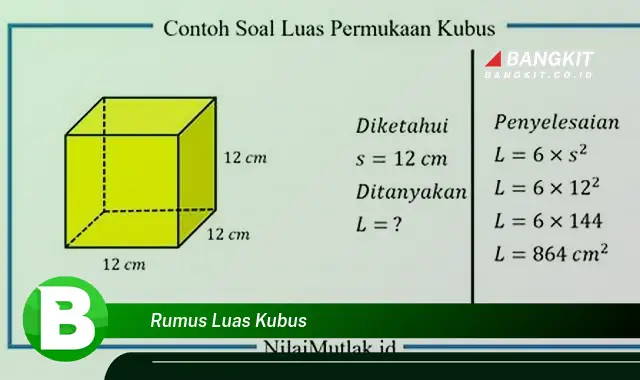
Rumus luas permukaan kubus adalah rumus yang digunakan untuk menghitung luas permukaan bangun ruang kubus. Rumus ini diperlukan untuk menghitung luas permukaan kubus dalam berbagai aplikasi, seperti menghitung luas permukaan sebuah kotak atau menghitung luas permukaan sebuah dadu.
Rumus luas permukaan kubus sangat penting karena memungkinkan kita untuk menghitung luas permukaan bangun ruang kubus secara akurat. Hal ini penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Selain itu, rumus luas permukaan kubus juga memiliki sejarah yang panjang, dengan catatan pertama penggunaan rumus ini ditemukan pada zaman Mesir Kuno.
Dalam artikel ini, kita akan membahas tentang rumus luas permukaan kubus, termasuk cara menggunakan rumus tersebut, pentingnya rumus tersebut, dan sejarah rumus tersebut. Kita juga akan membahas tentang aplikasi rumus luas permukaan kubus dalam berbagai bidang.
Rumus Luas Kubus
Rumus luas kubus merupakan rumus yang digunakan untuk menghitung luas permukaan bangun ruang kubus. Rumus ini sangat penting karena memungkinkan kita untuk menghitung luas permukaan kubus secara akurat dalam berbagai aplikasi.
- Panjang Sisi: Panjang sisi kubus merupakan faktor utama dalam menentukan luas permukaan kubus.
- Permukaan: Rumus luas permukaan kubus berkaitan dengan menghitung luas seluruh permukaan kubus.
- Volume: Luas permukaan kubus juga berkaitan dengan volume kubus, karena volume kubus dapat dihitung menggunakan luas permukaan kubus.
- Aplikasi: Rumus luas permukaan kubus memiliki banyak aplikasi dalam bidang teknik, arsitektur, dan desain.
- Sejarah: Rumus luas permukaan kubus memiliki sejarah yang panjang, dengan catatan pertama penggunaan rumus ini ditemukan pada zaman Mesir Kuno.
Kelima aspek ini saling terkait dan membentuk pemahaman yang komprehensif tentang rumus luas permukaan kubus. Memahami aspek-aspek ini sangat penting bagi siapa saja yang ingin menggunakan rumus ini secara efektif dalam berbagai aplikasi.
Panjang Sisi
Panjang sisi kubus merupakan faktor yang sangat penting dalam menentukan luas permukaan kubus. Hal ini karena luas permukaan kubus bergantung pada jumlah sisi kubus dan panjang sisi-sisinya. Semakin panjang sisi kubus, semakin besar luas permukaan kubusnya.
Sebagai contoh, jika sebuah kubus memiliki panjang sisi 1 cm, maka luas permukaan kubus tersebut adalah 6 cm2. Namun, jika panjang sisi kubus tersebut diperpanjang menjadi 2 cm, maka luas permukaan kubus tersebut menjadi 24 cm2. Hal ini menunjukkan bahwa panjang sisi kubus sangat berpengaruh terhadap luas permukaan kubus.
Memahami hubungan antara panjang sisi kubus dan luas permukaan kubus sangat penting dalam berbagai aplikasi. Misalnya, dalam teknik, arsitektur, dan desain, memahami hubungan ini sangat penting untuk menghitung kebutuhan material dan merencanakan struktur bangunan.
Permukaan
Rumus luas permukaan kubus memainkan peran penting dalam menentukan luas permukaan seluruh kubus. Rumus ini memungkinkan kita untuk menghitung luas setiap sisi kubus, lalu menjumlahkannya untuk mendapatkan luas permukaan total.
Sebagai contoh, misalkan sebuah kubus memiliki panjang sisi 5 cm. Untuk menghitung luas permukaan kubus ini, kita perlu menghitung luas setiap sisi terlebih dahulu. Luas setiap sisi adalah 5 cm x 5 cm = 25 cm2. Karena kubus memiliki 6 sisi, maka luas permukaan total kubus adalah 6 x 25 cm2 = 150 cm2.
Memahami hubungan antara rumus luas permukaan kubus dan luas permukaan kubus sangat penting dalam berbagai aplikasi. Misalnya, dalam bidang pengecatan, arsitektur, dan konstruksi, pemahaman ini sangat penting untuk memperkirakan jumlah bahan yang dibutuhkan dan merencanakan desain bangunan.
Volume
Hubungan antara luas permukaan kubus dan volume kubus sangatlah penting. Dengan mengetahui luas permukaan kubus, kita dapat menghitung volume kubus menggunakan rumus tertentu. Hal ini sangat berguna dalam berbagai aplikasi, seperti teknik, arsitektur, dan desain.
Sebagai contoh, misalkan sebuah tangki air berbentuk kubus memiliki luas permukaan 150 cm2. Untuk menghitung volume tangki air tersebut, kita dapat menggunakan rumus volume kubus, yaitu V = (L x L x L), dimana L adalah panjang sisi kubus. Karena luas permukaan kubus adalah 6 x L2, maka kita dapat menghitung panjang sisi kubus sebagai (150 cm2 / 6) = 5 cm. Dengan mengetahui panjang sisi kubus, kita dapat menghitung volume kubus sebagai 5 cm x 5 cm x 5 cm = 125 cm3.
Memahami hubungan antara luas permukaan kubus dan volume kubus sangat penting dalam berbagai aplikasi praktis. Misalnya, dalam bidang teknik, pemahaman ini digunakan untuk menghitung kapasitas tangki atau wadah lainnya. Dalam arsitektur, pemahaman ini digunakan untuk menghitung volume ruang atau bangunan.
Aplikasi
Rumus luas permukaan kubus memiliki banyak aplikasi penting dalam berbagai bidang, seperti teknik, arsitektur, dan desain. Dalam teknik, rumus ini digunakan untuk menghitung luas permukaan berbagai struktur dan komponen, seperti balok, pipa, dan tangki. Dalam arsitektur, rumus ini digunakan untuk menghitung luas permukaan bangunan, seperti rumah, gedung, dan jembatan. Dalam desain, rumus ini digunakan untuk menghitung luas permukaan berbagai produk, seperti kemasan, furnitur, dan peralatan.
Salah satu contoh penting dari aplikasi rumus luas permukaan kubus dalam teknik adalah dalam desain tangki penyimpanan. Untuk memastikan kapasitas tangki yang tepat, para insinyur perlu menghitung luas permukaan tangki dengan akurat. Hal ini karena luas permukaan tangki menentukan volume yang dapat ditampungnya. Dengan menggunakan rumus luas permukaan kubus, para insinyur dapat menghitung luas permukaan tangki dan menentukan volumenya dengan tepat.
Memahami hubungan antara rumus luas permukaan kubus dan aplikasi praktisnya sangat penting. Hal ini memungkinkan para profesional di berbagai bidang untuk merancang dan membangun struktur, bangunan, dan produk yang fungsional dan efisien.
Sejarah
Rumus luas permukaan kubus memiliki sejarah yang panjang dan kaya, yang ditelusuri kembali ke zaman Mesir Kuno. Bukti penggunaan rumus ini ditemukan pada Prasasti Matematika Rhind, gulungan papirus yang berasal dari sekitar tahun 2000-1800 SM. Gulungan ini berisi berbagai masalah matematika, termasuk cara menghitung luas permukaan kubus.
Pemahaman tentang rumus luas permukaan kubus sangat penting bagi perkembangan matematika dan arsitektur. Dalam peradaban Mesir Kuno, rumus ini digunakan untuk merancang dan membangun struktur seperti piramida dan kuil. Arsitek Mesir menggunakan rumus ini untuk memastikan bahwa struktur mereka stabil dan tahan lama.
Sepanjang sejarah, rumus luas permukaan kubus terus digunakan dan disempurnakan oleh para matematikawan dan ilmuwan. Rumus ini memainkan peran penting dalam pengembangan geometri dan kalkulus. Saat ini, rumus luas permukaan kubus digunakan dalam berbagai aplikasi, mulai dari teknik hingga desain industri.
Pertanyaan Umum Rumus Luas Kubus
Bagian ini akan membahas pertanyaan umum terkait rumus luas kubus, membantu Anda memahami konsep dan aplikasinya dengan lebih baik.
Pertanyaan 1: Apa pentingnya rumus luas kubus?
Rumus luas kubus sangat penting karena memungkinkan kita menghitung luas permukaan kubus secara akurat. Luas permukaan kubus diperlukan untuk berbagai aplikasi, seperti menghitung kebutuhan material, merencanakan desain bangunan, dan menentukan volume kubus.
Pertanyaan 2: Bagaimana cara menggunakan rumus luas kubus?
Rumus luas kubus adalah L^2 x 6, di mana L adalah panjang sisi kubus. Untuk menggunakan rumus ini, Anda perlu mengetahui panjang sisi kubus. Setelah itu, Anda cukup mengkuadratkan panjang sisi tersebut dan mengalikannya dengan 6.
Pertanyaan 3: Di bidang apa saja rumus luas kubus digunakan?
Rumus luas kubus digunakan dalam berbagai bidang, termasuk teknik, arsitektur, desain, dan matematika. Dalam teknik, rumus ini digunakan untuk menghitung luas permukaan struktur dan komponen. Dalam arsitektur, rumus ini digunakan untuk menghitung luas permukaan bangunan. Dalam desain, rumus ini digunakan untuk menghitung luas permukaan produk.
Pertanyaan 4: Apa saja faktor-faktor yang mempengaruhi luas permukaan kubus?
Luas permukaan kubus dipengaruhi oleh panjang sisinya. Semakin panjang sisi kubus, semakin besar luas permukaannya. Hal ini karena luas permukaan kubus berbanding lurus dengan kuadrat panjang sisinya.
Dengan memahami pertanyaan umum ini, Anda akan memiliki dasar yang kuat dalam memahami dan menerapkan rumus luas kubus dalam berbagai aplikasi.
Selanjutnya, kita akan membahas beberapa tips untuk menghitung luas permukaan kubus secara efektif.
Tips Menghitung Luas Permukaan Kubus
Berikut adalah beberapa tips untuk membantu Anda menghitung luas permukaan kubus secara efektif dan akurat:
Tip 1: Pahami Rumusnya
Rumus luas permukaan kubus adalah L^2 x 6, di mana L adalah panjang sisi kubus. Pastikan Anda memahami rumus ini dan cara menggunakannya sebelum memulai perhitungan.
Tip 2: Ukur Panjang Sisi dengan Tepat
Luas permukaan kubus sangat bergantung pada panjang sisinya. Oleh karena itu, penting untuk mengukur panjang sisi kubus dengan tepat menggunakan alat ukur yang sesuai, seperti penggaris atau jangka sorong.
Tip 3: Kuadratkan Panjang Sisi
Setelah Anda mengukur panjang sisi kubus, kuadratkan nilai tersebut dengan mengalikannya dengan dirinya sendiri. Langkah ini akan menghasilkan nilai yang akan digunakan dalam rumus luas permukaan kubus.
Tip 4: Kalikan dengan 6
Langkah terakhir adalah mengalikan nilai kuadrat panjang sisi dengan 6. Hasil perkalian ini akan memberikan Anda luas permukaan kubus.
Dengan mengikuti tips ini, Anda dapat menghitung luas permukaan kubus secara akurat dan efisien. Pemahaman yang kuat tentang rumus dan langkah-langkah perhitungan akan membantu Anda memastikan hasil yang tepat untuk aplikasi Anda.
