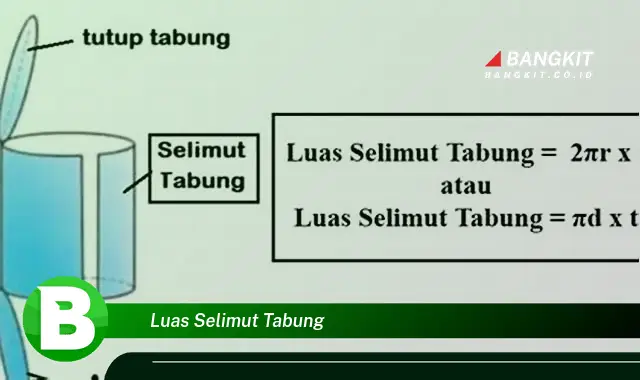
Luas selimut tabung adalah ukuran keliling selimut tabung, yaitu permukaan tabung yang melengkung. Rumus untuk menghitung luas selimut tabung adalah 2r x t, di mana (pi) adalah konstanta sekitar 3,14, r adalah jari-jari alas tabung, dan t adalah tinggi tabung.
Luas selimut tabung penting dalam berbagai bidang, seperti teknik dan fisika. Dalam teknik, luas selimut tabung digunakan untuk menghitung luas permukaan benda yang berbentuk tabung, seperti pipa dan tangki. Dalam fisika, luas selimut tabung digunakan untuk menghitung gaya yang bekerja pada benda yang bergerak dalam fluida, seperti hambatan udara pada pesawat terbang.
Konsep luas selimut tabung telah dikenal sejak zaman kuno. Ahli matematika Yunani Archimedes (287-212 SM) adalah salah satu orang pertama yang mempelajari luas selimut tabung. Penemuan Archimedes tentang luas selimut tabung sangat penting dalam pengembangan kalkulus.
Luas Selimut Tabung
Luas selimut tabung adalah ukuran keliling selimut tabung, yaitu permukaan tabung yang melengkung. Luas selimut tabung penting dalam berbagai bidang, seperti teknik dan fisika. Berikut adalah 5 aspek penting terkait luas selimut tabung:
- Rumus: 2rt
- Satuan: cm, m, dll.
- Aplikasi: Menghitung luas permukaan benda berbentuk tabung
- Sejarah: Ditemukan oleh Archimedes
- Relevansi: Berguna dalam teknik dan fisika
Kelima aspek ini saling terkait dan membentuk pemahaman yang komprehensif tentang luas selimut tabung. Rumus luas selimut tabung digunakan untuk menghitung luas permukaan benda berbentuk tabung, seperti pipa dan tangki. Satuan luas selimut tabung harus sesuai dengan satuan panjang yang digunakan, misalnya cm atau m. Aplikasi luas selimut tabung sangat luas, mulai dari teknik hingga fisika. Sejarah penemuan luas selimut tabung oleh Archimedes menunjukkan pentingnya konsep ini sejak zaman kuno. Relevansi luas selimut tabung dalam teknik dan fisika menunjukkan bahwa konsep ini memiliki nilai praktis yang tinggi.
Rumus
Rumus 2rt adalah rumus untuk menghitung luas selimut tabung, yaitu permukaan tabung yang melengkung. Rumus ini menghubungkan keliling alas tabung (2r) dengan tinggi tabung (t), sehingga memungkinkan kita untuk menentukan luas permukaan tabung secara efisien.
- Menghitung Luas Permukaan Tabung: Rumus 2rt digunakan secara luas untuk menghitung luas permukaan tabung dalam berbagai aplikasi, seperti menghitung luas permukaan pipa, tangki, dan kaleng.
- Perbandingan Tabung Berbeda: Rumus ini dapat digunakan untuk membandingkan luas selimut tabung dengan ukuran berbeda. Tabung dengan jari-jari alas lebih besar atau tinggi lebih besar akan memiliki luas selimut yang lebih besar.
- Aplikasi dalam Desain: Dalam bidang desain, rumus 2rt digunakan untuk menentukan dimensi tabung yang diperlukan untuk mencapai luas permukaan tertentu, seperti dalam desain pipa dan bejana.
- Relevansi dalam Bidang Lain: Konsep luas selimut tabung dan rumus 2rt juga relevan dalam bidang lain, seperti fisika dan teknik, untuk menghitung gaya dan tekanan yang bekerja pada benda berbentuk tabung.
Dengan memahami rumus 2rt dan kaitannya dengan luas selimut tabung, kita dapat memperoleh pemahaman yang lebih baik tentang sifat tabung dan menerapkannya dalam berbagai aplikasi praktis dan teoretis.
Satuan
Dalam konteks luas selimut tabung, satuan yang digunakan untuk menyatakan luas sangatlah penting. Satuan yang umum digunakan antara lain cm2 (sentimeter persegi), m2 (meter persegi), dan satuan turunan lainnya yang sesuai.
- Standarisasi Pengukuran: Satuan luas yang tepat memastikan bahwa pengukuran luas selimut tabung dapat distandarisasi dan dikomunikasikan secara jelas, memungkinkan perbandingan dan perhitungan yang akurat.
- Aplikasi Praktis: Dalam aplikasi praktis, satuan luas yang sesuai dipilih berdasarkan konteks dan skala tabung yang diukur. Misalnya, cm2 digunakan untuk tabung kecil, sedangkan m2 digunakan untuk tabung berukuran lebih besar.
- Konversi Satuan: Terkadang, diperlukan konversi antara satuan luas yang berbeda untuk memenuhi kebutuhan tertentu. Konversi ini dapat dilakukan menggunakan faktor konversi yang sesuai.
- Pemahaman Konsep: Memahami satuan luas yang digunakan untuk menyatakan luas selimut tabung sangat penting untuk interpretasi yang benar dari hasil perhitungan dan pengukuran.
Dengan memahami pentingnya satuan luas dan penggunaannya yang tepat, kita dapat memastikan akurasi dan kejelasan dalam pengukuran dan perhitungan yang melibatkan luas selimut tabung.
Aplikasi
Luas selimut tabung memainkan peran penting dalam menghitung luas permukaan benda berbentuk tabung. Benda berbentuk tabung banyak ditemukan dalam kehidupan sehari-hari, seperti pipa, tangki, dan kaleng.
- Menghitung Luas Permukaan Pipa: Luas selimut tabung digunakan untuk menentukan luas permukaan pipa, yang penting untuk menghitung kehilangan panas, tekanan fluida, dan aliran fluida.
- Menentukan Luas Permukaan Tangki: Tangki berbentuk tabung umum digunakan untuk menyimpan cairan dan gas. Luas selimut tabung membantu menentukan luas permukaan tangki, yang diperlukan untuk menghitung kapasitas dan ketahanan strukturnya.
- Mengetahui Luas Permukaan Kaleng: Luas selimut tabung digunakan dalam industri pengemasan untuk menghitung luas permukaan kaleng, yang berdampak pada biaya bahan dan pelabelan produk.
- Membandingkan Luas Tabung Berbeda: Luas selimut tabung memungkinkan perbandingan luas permukaan tabung dengan ukuran atau bentuk berbeda, yang berguna dalam optimalisasi desain dan pemilihan bahan.
Dengan memahami aplikasi luas selimut tabung dalam menghitung luas permukaan benda berbentuk tabung, kita dapat menghargai pentingnya konsep ini dalam berbagai bidang, mulai dari teknik hingga industri.
Sejarah
Penemuan luas selimut tabung oleh Archimedes sekitar tahun 250 SM menandai titik awal penting dalam sejarah matematika dan fisika. Archimedes, seorang matematikawan dan fisikawan Yunani kuno, diakui atas kontribusinya yang luar biasa pada berbagai bidang, termasuk geometri dan hidrostatika.
- Pemahaman Geometris: Penemuan luas selimut tabung menunjukkan pemahaman Archimedes yang mendalam tentang geometri dan sifat-sifat tabung. Ia mampu mengidentifikasi hubungan antara keliling alas dan tinggi tabung dengan luas permukaannya.
- Aplikasi Praktis: Penemuan Archimedes memiliki aplikasi praktis dalam berbagai bidang, seperti teknik dan arsitektur. Luas selimut tabung digunakan untuk menghitung luas permukaan benda berbentuk tabung, seperti pipa dan kolom.
- Dasar Kalkulus Integral: Penemuan Archimedes tentang luas selimut tabung menjadi dasar pengembangan kalkulus integral, sebuah cabang matematika yang berurusan dengan penjumlahan batas jumlah yang tak terhingga kecil. Ini memungkinkan perhitungan luas permukaan dan volume bentuk yang lebih kompleks.
- Warisan Abadi: Penemuan Archimedes tentang luas selimut tabung terus menjadi landasan dalam matematika dan fisika hingga hari ini. Hal ini menjadi bukti kejeniusan dan kontribusinya yang bertahan lama pada pemahaman kita tentang dunia.
Penemuan Archimedes tentang luas selimut tabung tidak hanya merupakan pencapaian intelektual yang signifikan tetapi juga memiliki dampak yang langgeng pada perkembangan matematika dan aplikasinya dalam dunia nyata.
Relevansi
Luas selimut tabung memiliki relevansi yang tinggi dalam bidang teknik dan fisika karena penggunaannya yang luas dalam perhitungan dan aplikasi praktis.
-
Perhitungan Teknis
Dalam teknik, luas selimut tabung digunakan untuk menghitung luas permukaan benda berbentuk tabung, seperti pipa, tangki, dan bejana tekan. Perhitungan ini penting untuk menentukan kebutuhan material, efisiensi perpindahan panas, dan kekuatan struktural.
-
Analisis Hidrodinamika
Dalam fisika, khususnya hidrodinamika, luas selimut tabung digunakan untuk menghitung gaya hambat pada benda yang bergerak dalam fluida. Gaya hambat ini penting dalam desain kapal, pesawat terbang, dan kendaraan yang bergerak melalui air atau udara.
-
Perpindahan Panas
Luas selimut tabung juga berperan dalam perhitungan perpindahan panas. Dalam bidang teknik mesin dan kimia, luas selimut tabung digunakan untuk menentukan laju perpindahan panas antara fluida dan permukaan tabung, yang penting dalam desain penukar panas dan reaktor kimia.
-
Aplikasi Elektromagnetik
Dalam fisika elektromagnetik, luas selimut tabung digunakan untuk menghitung induktansi kumparan solenoida. Induktansi ini menentukan kemampuan kumparan untuk menyimpan energi magnetik, yang penting dalam aplikasi seperti motor listrik dan transformator.
Relevansi luas selimut tabung dalam teknik dan fisika sangatlah luas dan menyentuh berbagai bidang, mulai dari desain struktural hingga analisis fluida dan elektromagnetisme. Pemahaman yang baik tentang konsep ini sangat penting bagi para insinyur, fisikawan, dan ilmuwan yang bekerja di bidang-bidang ini.
FAQ Luas Selimut Tabung
Berikut adalah beberapa pertanyaan umum dan jawabannya mengenai luas selimut tabung:
Pertanyaan 1: Bagaimana cara menghitung luas selimut tabung?
Jawaban: Luas selimut tabung dapat dihitung menggunakan rumus 2r x t, di mana adalah konstanta sekitar 3,14, r adalah jari-jari alas tabung, dan t adalah tinggi tabung.
Pertanyaan 2: Apa satuan luas selimut tabung?
Jawaban: Satuan luas selimut tabung adalah satuan luas, seperti cm2 (sentimeter persegi) atau m2 (meter persegi).
Pertanyaan 3: Di bidang apa saja luas selimut tabung digunakan?
Jawaban: Luas selimut tabung digunakan dalam berbagai bidang, seperti teknik, fisika, dan matematika, untuk menghitung luas permukaan benda berbentuk tabung, gaya hambat pada benda yang bergerak dalam fluida, dan induktansi kumparan solenoida.
Pertanyaan 4: Siapa yang menemukan rumus luas selimut tabung?
Jawaban: Rumus luas selimut tabung ditemukan oleh Archimedes, seorang matematikawan dan fisikawan Yunani kuno.
Kesimpulan:
Memahami luas selimut tabung dan cara menghitungnya sangat penting dalam berbagai bidang. Rumus luas selimut tabung, satuannya, dan aplikasinya harus dipahami dengan baik untuk melakukan perhitungan dan analisis yang akurat.
Tips:
Untuk mempelajari lebih lanjut tentang luas selimut tabung, Anda dapat membaca buku teks matematika atau fisika, mencari sumber daya online, atau berkonsultasi dengan ahli di bidang terkait.
Tips Mempelajari Luas Selimut Tabung
Untuk memahami luas selimut tabung dengan lebih baik, berikut beberapa tips yang dapat dipertimbangkan:
Tip 1: Kuasai Rumus
Pahami dan hafalkan rumus luas selimut tabung, yaitu 2rt, di mana adalah konstanta sekitar 3,14, r adalah jari-jari alas tabung, dan t adalah tinggi tabung. Memahami rumus ini sangat penting untuk menghitung luas selimut tabung secara akurat.
Tip 2: Latihan Soal
Latih diri Anda dengan mengerjakan banyak soal yang berkaitan dengan luas selimut tabung. Ini akan membantu Anda menguasai penerapan rumus dan meningkatkan keterampilan pemecahan masalah Anda.
Tip 3: Visualisasikan Konsep
Bayangkan sebuah tabung dan bagian permukaannya yang melengkung. Visualisasi ini dapat membantu Anda memahami konsep luas selimut tabung dan bagaimana rumus tersebut diturunkan.
Tip 4: Terapkan dalam Konteks
Jelajahi berbagai aplikasi luas selimut tabung dalam bidang teknik, fisika, dan matematika. Memahami konteks penggunaannya akan memperdalam pemahaman Anda tentang konsep ini.
Dengan mengikuti tips ini, Anda dapat meningkatkan pemahaman Anda tentang luas selimut tabung dan menerapkannya secara efektif dalam berbagai situasi.
