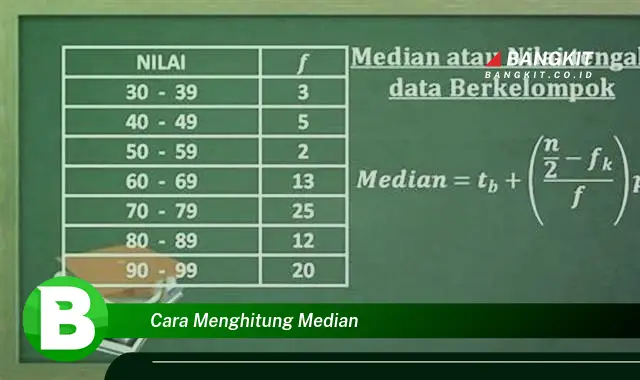
Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan dari yang terkecil hingga terbesar. Median dapat digunakan untuk mengetahui nilai tengah suatu data tanpa terpengaruh oleh nilai ekstrem, seperti nilai terbesar atau terkecil. Cara menghitung median sangat mudah, yaitu dengan mengambil nilai tengah dari data yang telah diurutkan. Jika jumlah data ganjil, maka median adalah nilai tengahnya. Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengahnya.
Median sangat penting dalam statistik karena dapat memberikan gambaran yang lebih akurat tentang nilai tengah data dibandingkan dengan mean (rata-rata). Hal ini karena median tidak terpengaruh oleh nilai ekstrem, sementara mean dapat terpengaruh oleh nilai ekstrem. Median juga lebih mudah dihitung dibandingkan dengan mean, sehingga sering digunakan dalam aplikasi praktis.
Median memiliki sejarah panjang dalam statistik. Konsep median pertama kali diperkenalkan oleh Thomas Simpson pada tahun 1755. Median kemudian dikembangkan lebih lanjut oleh Karl Pearson dan Francis Galton pada akhir abad ke-19. Median sekarang menjadi salah satu ukuran statistik yang paling umum digunakan dan diajarkan di seluruh dunia.
Cara Menghitung Median
Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan. Median dapat digunakan untuk mengetahui nilai tengah suatu data tanpa terpengaruh oleh nilai ekstrem, seperti nilai terbesar atau terkecil. Cara menghitung median sangat mudah, yaitu dengan mengambil nilai tengah dari data yang telah diurutkan. Jika jumlah data ganjil, maka median adalah nilai tengahnya. Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengahnya.
- Mengurutkan data
- Mencari nilai tengah
- Mengambil nilai tengah
- Menghitung rata-rata dua nilai tengah
Sebagai contoh, jika kita memiliki data {1, 3, 5, 7, 9}, maka mediannya adalah 5. Hal ini karena 5 adalah nilai tengah dari data tersebut. Jika kita memiliki data {1, 3, 5, 7, 9, 11}, maka mediannya adalah 6. Hal ini karena 6 adalah rata-rata dari dua nilai tengah, yaitu 5 dan 7.
Median sangat penting dalam statistik karena dapat memberikan gambaran yang lebih akurat tentang nilai tengah data dibandingkan dengan mean (rata-rata). Hal ini karena median tidak terpengaruh oleh nilai ekstrem, sementara mean dapat terpengaruh oleh nilai ekstrem. Median juga lebih mudah dihitung dibandingkan dengan mean, sehingga sering digunakan dalam aplikasi praktis.
Mengurutkan Data
Mengurutkan data merupakan langkah penting dalam menghitung median. Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan. Dengan mengurutkan data, kita dapat dengan mudah menentukan nilai tengah tersebut.
- Urutkan data dari yang terkecil hingga terbesar.
- Jika jumlah data ganjil, maka median adalah nilai tengahnya.
- Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengahnya.
Sebagai contoh, jika kita memiliki data {1, 3, 5, 7, 9}, maka kita dapat mengurutkannya menjadi {1, 3, 5, 7, 9}. Karena jumlah data ganjil, maka mediannya adalah 5, yaitu nilai tengahnya. Jika kita memiliki data {1, 3, 5, 7, 9, 11}, maka kita dapat mengurutkannya menjadi {1, 3, 5, 7, 9, 11}. Karena jumlah data genap, maka mediannya adalah (5 + 7) / 2 = 6, yaitu rata-rata dari dua nilai tengahnya.
Mengurutkan data juga penting untuk menghitung statistik lainnya, seperti mean (rata-rata), modus (nilai yang paling sering muncul), dan jangkauan (selisih antara nilai terbesar dan terkecil). Dengan mengurutkan data, kita dapat dengan mudah mengidentifikasi nilai-nilai ini dan memahami distribusi data.
Mencari Nilai Tengah
Mencari nilai tengah merupakan langkah penting dalam menghitung median. Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan. Dengan mencari nilai tengah, kita dapat dengan mudah menentukan nilai median tersebut.
-
Mencari nilai tengah dari data ganjil
Jika jumlah data ganjil, maka nilai tengahnya adalah nilai yang terletak di tengah-tengah data setelah diurutkan.
-
Mencari nilai tengah dari data genap
Jika jumlah data genap, maka nilai tengahnya adalah rata-rata dari dua nilai yang terletak di tengah-tengah data setelah diurutkan.
Mencari nilai tengah juga penting untuk menghitung statistik lainnya, seperti mean (rata-rata), modus (nilai yang paling sering muncul), dan jangkauan (selisih antara nilai terbesar dan terkecil). Dengan mencari nilai tengah, kita dapat dengan mudah mengidentifikasi nilai-nilai ini dan memahami distribusi data.
Mengambil Nilai Tengah
Mengambil nilai tengah adalah langkah penting dalam cara menghitung median. Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan. Dengan mengambil nilai tengah, kita dapat dengan mudah menentukan nilai median tersebut.
-
Mencari Nilai Tengah dari Data Ganjil
Jika jumlah data ganjil, maka nilai tengahnya adalah nilai yang terletak di tengah-tengah data setelah diurutkan. Sebagai contoh, jika kita memiliki data {1, 3, 5, 7, 9}, maka nilai tengahnya adalah 5, yaitu nilai yang terletak di tengah-tengah data setelah diurutkan.
-
Mencari Nilai Tengah dari Data Genap
Jika jumlah data genap, maka nilai tengahnya adalah rata-rata dari dua nilai yang terletak di tengah-tengah data setelah diurutkan. Sebagai contoh, jika kita memiliki data {1, 3, 5, 7, 9, 11}, maka nilai tengahnya adalah (5 + 7) / 2 = 6, yaitu rata-rata dari dua nilai yang terletak di tengah-tengah data setelah diurutkan.
Mengambil nilai tengah juga penting untuk menghitung statistik lainnya, seperti mean (rata-rata), modus (nilai yang paling sering muncul), dan jangkauan (selisih antara nilai terbesar dan terkecil). Dengan mengambil nilai tengah, kita dapat dengan mudah mengidentifikasi nilai-nilai ini dan memahami distribusi data.
Menghitung Rata-rata Dua Nilai Tengah
Dalam konteks penghitungan median, menghitung rata-rata dua nilai tengah merupakan langkah penting ketika jumlah data yang dimiliki genap. Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan, dan ketika jumlah data genap, tidak ada satu nilai tengah yang jelas. Oleh karena itu, digunakanlah rata-rata dua nilai tengah untuk mewakili median.
-
Menentukan Nilai Tengah
Langkah pertama adalah menentukan dua nilai tengah dari data yang telah diurutkan. Nilai tengah adalah nilai yang terletak di tengah-tengah data, atau tepat di sebelah kiri dan kanan nilai tengah jika jumlah data genap.
-
Menghitung Rata-rata
Setelah dua nilai tengah ditentukan, langkah selanjutnya adalah menghitung rata-ratanya. Rata-rata dapat dihitung dengan menjumlahkan kedua nilai tengah dan membaginya dengan dua.
-
Median
Nilai yang diperoleh dari penghitungan rata-rata dua nilai tengah inilah yang disebut sebagai median. Median mewakili nilai tengah dari data yang genap, tidak terpengaruh oleh nilai ekstrem, dan memberikan gambaran yang lebih akurat tentang nilai tengah data dibandingkan dengan mean (rata-rata).
Sebagai contoh, jika kita memiliki data {1, 3, 5, 7, 9, 11}, maka mediannya adalah (5 + 7) / 2 = 6. Nilai 5 dan 7 adalah dua nilai tengah dari data tersebut, dan rata-ratanya adalah 6. Oleh karena itu, median dari data tersebut adalah 6.
Tanya Jawab Seputar Cara Menghitung Median
Berikut adalah beberapa pertanyaan yang sering diajukan beserta jawabannya mengenai cara menghitung median:
Pertanyaan 1: Apa itu median?
Jawaban: Median adalah nilai tengah dari suatu kumpulan data yang telah diurutkan dari yang terkecil hingga terbesar.
Pertanyaan 2: Bagaimana cara menghitung median?
Jawaban: Untuk menghitung median, urutkan terlebih dahulu data dari yang terkecil hingga terbesar. Jika jumlah data ganjil, median adalah nilai tengahnya. Jika jumlah data genap, median adalah rata-rata dari dua nilai tengahnya.
Pertanyaan 3: Apa perbedaan antara median dan mean?
Jawaban: Median adalah nilai tengah dari data yang telah diurutkan, sedangkan mean (rata-rata) adalah jumlah semua nilai data dibagi dengan jumlah data. Median tidak terpengaruh oleh nilai ekstrem, sedangkan mean dapat terpengaruh oleh nilai ekstrem.
Pertanyaan 4: Kapan median digunakan?
Jawaban: Median digunakan ketika kita ingin mengetahui nilai tengah suatu data tanpa terpengaruh oleh nilai ekstrem. Median sering digunakan dalam statistik untuk memberikan gambaran yang lebih akurat tentang nilai tengah data.
Kesimpulan: Median merupakan ukuran statistik yang penting untuk mengetahui nilai tengah suatu data. Median mudah untuk dihitung dan tidak terpengaruh oleh nilai ekstrem.
Tips: Untuk menghitung median dengan cepat dan mudah, gunakan kalkulator statistik atau spreadsheet.
Tips Menghitung Median
Berikut adalah beberapa tips untuk menghitung median dengan mudah dan akurat:
Tip 1: Urutkan Data
Sebelum menghitung median, urutkan terlebih dahulu data dari yang terkecil hingga terbesar. Pengurutan data akan memudahkan Anda dalam menentukan nilai tengah.
Tip 2: Tentukan Jumlah Data
Setelah data diurutkan, tentukan apakah jumlah data ganjil atau genap. Jika jumlah data ganjil, maka median adalah nilai tengahnya. Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengahnya.
Tip 3: Cari Nilai Tengah
Nilai tengah adalah nilai yang terletak di tengah-tengah data yang telah diurutkan. Jika jumlah data ganjil, nilai tengahnya adalah satu nilai. Jika jumlah data genap, nilai tengahnya adalah dua nilai yang berdampingan.
Tip 4: Hitung Median
Jika jumlah data ganjil, maka median adalah nilai tengahnya. Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengahnya. Median dapat dihitung dengan menjumlahkan dua nilai tengah dan membaginya dengan dua.
Kesimpulan: Dengan mengikuti tips ini, Anda dapat menghitung median dengan mudah dan akurat. Median merupakan ukuran statistik yang penting untuk mengetahui nilai tengah suatu data.
