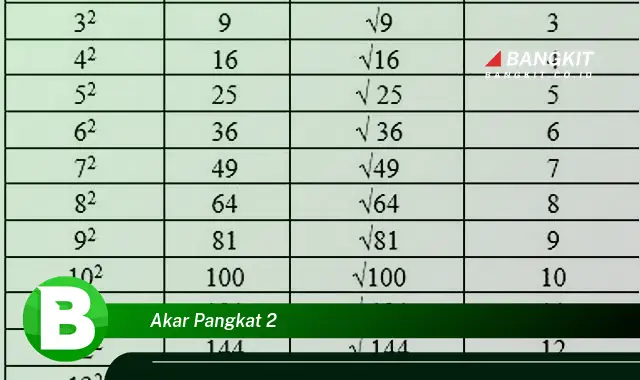
Akar pangkat 2, juga dikenal sebagai akar kuadrat, adalah operasi matematika yang digunakan untuk mencari nilai yang, ketika dikalikan dengan dirinya sendiri, menghasilkan angka tertentu. Dalam notasi matematika, akar pangkat 2 dari sebuah angka a dinyatakan sebagai a. Misalnya, akar pangkat 2 dari 9 adalah 3, karena 3 x 3 = 9.
Akar pangkat 2 memiliki peran penting dalam berbagai bidang, termasuk matematika, fisika, dan teknik. Ini digunakan untuk menyelesaikan persamaan kuadrat, menghitung jarak, dan menentukan luas dan volume bangun ruang. Pengetahuan tentang akar pangkat 2 sangat penting untuk pemahaman yang kuat tentang matematika dasar dan aplikasinya di dunia nyata.
Dalam artikel ini, kita akan membahas konsep akar pangkat 2 secara lebih mendalam, termasuk metode untuk menghitungnya, sifat-sifatnya, dan aplikasinya dalam berbagai bidang. Kami juga akan mengeksplorasi sejarah akar pangkat 2 dan kontribusi para matematikawan terkemuka terhadap perkembangannya.
Akar Pangkat 2
Akar pangkat 2, atau akar kuadrat, adalah operasi matematika dasar yang sangat penting dalam berbagai bidang. Berikut adalah lima aspek penting yang terkait dengan akar pangkat 2:
- Definisi: Akar pangkat 2 dari suatu bilangan adalah nilai yang, ketika dikalikan dengan dirinya sendiri, menghasilkan bilangan tersebut.
- Notasi: Akar pangkat 2 dari suatu bilangan a dinotasikan sebagai a.
- Metode Penghitungan: Akar pangkat 2 dapat dihitung menggunakan berbagai metode, seperti faktorisasi prima, pembagian panjang, dan kalkulator.
- Sifat: Akar pangkat 2 memiliki sifat-sifat tertentu, seperti selalu menghasilkan bilangan positif untuk bilangan positif, dan menghasilkan 0 untuk 0.
- Aplikasi: Akar pangkat 2 memiliki banyak aplikasi dalam matematika, fisika, teknik, dan bidang lainnya, seperti menyelesaikan persamaan kuadrat, menghitung jarak, dan menentukan luas dan volume.
Kelima aspek ini bersama-sama memberikan pemahaman dasar yang kuat tentang konsep akar pangkat 2. Dengan memahami definisi, notasi, metode penghitungan, sifat, dan aplikasinya, kita dapat menggunakan akar pangkat 2 secara efektif dalam berbagai situasi.
Definisi
Definisi ini sangat penting karena memberikan pemahaman mendasar tentang konsep akar pangkat 2. Dengan memahami definisi ini, kita dapat memperoleh wawasan tentang sifat dan aplikasi akar pangkat 2.
-
Menemukan akar kuadrat bilangan bulat sempurna
Salah satu aplikasi dasar dari definisi akar pangkat 2 adalah menemukan akar kuadrat dari bilangan bulat sempurna. Misalnya, akar kuadrat dari 16 adalah 4 karena 4 x 4 = 16. -
Menyelesaikan persamaan kuadrat
Akar pangkat 2 juga berperan penting dalam menyelesaikan persamaan kuadrat, yang merupakan persamaan bentuk ax + bx + c = 0. Dengan menggunakan rumus kuadrat, kita dapat menemukan akar-akar persamaan kuadrat dengan menghitung akar pangkat 2 dari diskriminan. -
Menghitung jarak
Akar pangkat 2 juga digunakan dalam menghitung jarak dalam geometri. Misalnya, untuk mencari jarak antara dua titik (x1, y1) dan (x2, y2), kita dapat menggunakan rumus jarak: jarak = ((x2 – x1) + (y2 – y1)). Rumus ini melibatkan penghitungan akar pangkat 2 dari selisih koordinat kedua titik. -
Menentukan luas dan volume
Akar pangkat 2 juga digunakan dalam menentukan luas dan volume bangun ruang. Misalnya, untuk mencari luas persegi, kita dapat menggunakan rumus luas = sisi, yang melibatkan menghitung akar pangkat 2 dari panjang sisi persegi.
Dengan memahami definisi akar pangkat 2 dan aplikasinya yang luas, kita dapat menghargai pentingnya operasi matematika dasar ini dalam berbagai bidang, termasuk matematika, fisika, teknik, dan banyak lagi.
Notasi
Notasi akar pangkat 2 memegang peranan penting dalam matematika. Notasi $\sqrt{a}$ menunjukkan akar pangkat 2 dari sebuah bilangan $a$. Notasi ini memberikan bentuk yang ringkas dan jelas untuk mengekspresikan operasi akar pangkat 2.
- Representasi Matematis: Notasi $\sqrt{a}$ memberikan representasi matematis yang ringkas dan mudah dipahami untuk akar pangkat 2. Notasi ini memungkinkan penulisan persamaan dan operasi matematika yang melibatkan akar pangkat 2 dengan cara yang jelas dan efisien.
- Perhitungan Mudah: Notasi $\sqrt{a}$ menyederhanakan perhitungan akar pangkat 2. Dengan menggunakan kalkulator atau tabel matematika, kita dapat dengan mudah mengevaluasi nilai $\sqrt{a}$ untuk berbagai bilangan $a$.
- Sifat Akar Pangkat 2: Notasi $\sqrt{a}$ membantu kita memahami sifat-sifat akar pangkat 2. Misalnya, kita dapat melihat bahwa $\sqrt{a^2} = a$ dan $(\sqrt{a})^2 = a$. Sifat-sifat ini memudahkan kita dalam memanipulasi dan menyederhanakan ekspresi yang melibatkan akar pangkat 2.
- Aplikasi Luas: Notasi $\sqrt{a}$ memiliki aplikasi yang luas dalam berbagai bidang, seperti fisika, teknik, dan keuangan. Dalam fisika, notasi ini digunakan untuk menghitung kecepatan dan percepatan. Dalam teknik, notasi ini digunakan untuk merancang sirkuit listrik dan struktur. Dalam keuangan, notasi ini digunakan untuk menghitung pengembalian investasi dan risiko.
Dengan memahami notasi $\sqrt{a}$, kita dapat memanfaatkan akar pangkat 2 secara efektif dalam berbagai aplikasi matematika dan bidang lainnya.
Metode Penghitungan
Metode penghitungan akar pangkat 2 sangat penting karena memungkinkan kita untuk menentukan nilai akar pangkat 2 dari suatu bilangan dengan akurat dan efisien. Metode-metode ini memanfaatkan prinsip-prinsip matematika untuk menyederhanakan proses dan memperoleh hasil yang tepat.
Misalnya, dalam faktorisasi prima, kita menguraikan bilangan menjadi faktor-faktor primanya dan kemudian menggunakan sifat-sifat akar untuk menyederhanakan perhitungan. Demikian pula, pembagian panjang memberikan pendekatan bertahap untuk menemukan akar pangkat 2 dari bilangan besar.
Selain metode manual ini, kalkulator dan komputer menyediakan cara yang cepat dan akurat untuk menghitung akar pangkat 2. Alat-alat ini menggunakan algoritma canggih untuk memberikan hasil yang sangat tepat dalam hitungan detik.
Memahami metode penghitungan akar pangkat 2 sangat penting untuk berbagai aplikasi praktis. Dalam teknik, akar pangkat 2 digunakan untuk menghitung panjang diagonal, gaya, dan tegangan. Dalam keuangan, akar pangkat 2 digunakan untuk menghitung pengembalian investasi dan manajemen risiko.
Dengan menguasai metode penghitungan akar pangkat 2, kita dapat memanfaatkan konsep matematika dasar ini untuk memecahkan masalah di berbagai bidang, meningkatkan efisiensi dan akurasi dalam pengambilan keputusan.
Sifat
Sifat-sifat akar pangkat 2 sangat penting karena memberikan dasar yang kuat untuk memahami dan menggunakan operasi matematika ini secara efektif. Sifat-sifat ini menjelaskan karakteristik unik dari akar pangkat 2 dan membedakannya dari operasi matematika lainnya.
-
Selalu menghasilkan bilangan positif untuk bilangan positif
Salah satu sifat penting dari akar pangkat 2 adalah selalu menghasilkan bilangan positif ketika diterapkan pada bilangan positif. Misalnya, akar pangkat 2 dari 25 adalah 5 karena 5 x 5 = 25. Sifat ini sangat berguna dalam aplikasi praktis, seperti menghitung panjang sisi persegi atau jarak antara dua titik. -
Menghasilkan 0 untuk 0
Sifat penting lainnya dari akar pangkat 2 adalah menghasilkan 0 ketika diterapkan pada 0. Misalnya, akar pangkat 2 dari 0 adalah 0 karena 0 x 0 = 0. Sifat ini konsisten dengan sifat perkalian bilangan, dimana mengalikan bilangan apa pun dengan 0 selalu menghasilkan 0. -
Tidak didefinisikan untuk bilangan negatif
Secara umum, akar pangkat 2 tidak didefinisikan untuk bilangan negatif. Hal ini karena hasil kali dua bilangan negatif adalah bilangan positif, dan tidak ada bilangan negatif yang, ketika dikalikan dengan dirinya sendiri, menghasilkan bilangan positif. -
Memiliki sifat komutatif dan asosiatif
Akar pangkat 2 memiliki sifat komutatif dan asosiatif, yang berarti urutan akar tidak mempengaruhi hasil. Artinya, $\sqrt{ab} = \sqrt{a} \times \sqrt{b}$ dan $\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}$ .
Dengan memahami sifat-sifat akar pangkat 2 ini, kita dapat menggunakannya dengan percaya diri dalam berbagai aplikasi, memastikan hasil yang akurat dan bermakna. Sifat-sifat ini membentuk dasar untuk eksplorasi lebih lanjut dan penerapan akar pangkat 2 dalam matematika, sains, dan bidang lainnya.
Aplikasi
Akar pangkat 2 memiliki peran penting dalam berbagai aplikasi karena sifat-sifatnya yang unik dan kemampuannya untuk menyelesaikan masalah matematika dan fisika yang kompleks. Sifat-sifat ini menjadikannya alat yang sangat berharga dalam berbagai bidang, seperti:
- Matematika: Akar pangkat 2 digunakan dalam menyelesaikan persamaan kuadrat, yang merupakan persamaan umum yang muncul dalam berbagai masalah matematika. Akar pangkat 2 juga digunakan dalam trigonometri untuk menghitung panjang sisi segitiga siku-siku dan sudutnya.
- Fisika: Akar pangkat 2 digunakan dalam menghitung kecepatan, percepatan, dan gaya. Misalnya, persamaan gerak yang terkenal, v = u + at, menggunakan akar pangkat 2 untuk menghitung kecepatan akhir (v) suatu benda.
- Teknik: Akar pangkat 2 digunakan dalam merancang jembatan, bangunan, dan mesin. Misalnya, dalam analisis struktur, akar pangkat 2 digunakan untuk menghitung tegangan dan regangan pada material.
- Bidang lainnya: Akar pangkat 2 juga digunakan dalam berbagai bidang lain, seperti keuangan untuk menghitung suku bunga dan investasi, dan biologi untuk menghitung pertumbuhan populasi dan laju reaksi kimia.
Memahami aplikasi akar pangkat 2 sangat penting karena memungkinkan kita untuk memanfaatkan kekuatan operasi matematika ini untuk memecahkan masalah di berbagai bidang. Dengan menguasai konsep akar pangkat 2 dan aplikasinya, kita dapat meningkatkan keterampilan berpikir kritis, pemecahan masalah, dan pengambilan keputusan kita.
Pertanyaan Umum tentang Akar Pangkat 2
Berikut adalah beberapa pertanyaan umum dan jawabannya tentang akar pangkat 2:
Pertanyaan 1: Apa itu akar pangkat 2?
Akar pangkat 2, juga dikenal sebagai akar kuadrat, adalah operasi matematika yang digunakan untuk mencari nilai yang, ketika dikalikan dengan dirinya sendiri, menghasilkan angka tertentu.
Pertanyaan 2: Bagaimana cara menghitung akar pangkat 2?
Ada beberapa metode untuk menghitung akar pangkat 2, yaitu dengan menggunakan kalkulator, pembagian panjang, atau faktorisasi prima.
Pertanyaan 3: Apa saja sifat-sifat akar pangkat 2?
Sifat-sifat akar pangkat 2 antara lain selalu menghasilkan bilangan positif untuk bilangan positif, menghasilkan 0 untuk 0, dan tidak terdefinisi untuk bilangan negatif.
Pertanyaan 4: Di mana saja akar pangkat 2 digunakan?
Akar pangkat 2 memiliki banyak aplikasi dalam matematika, fisika, teknik, dan bidang lainnya, seperti menyelesaikan persamaan kuadrat, menghitung jarak, dan menentukan luas dan volume.
Dengan memahami konsep dan sifat akar pangkat 2, kita dapat menggunakannya secara efektif untuk memecahkan berbagai masalah matematika dan fisika.
Silakan lanjutkan membaca untuk tips menggunakan akar pangkat 2 dalam praktik.
Tips Menggunakan Akar Pangkat 2
Setelah memahami konsep dan sifat akar pangkat 2, berikut adalah beberapa tips untuk menggunakannya secara efektif dalam praktik:
Tip 1: Gunakan kalkulator atau tabel matematika
Untuk menghitung akar pangkat 2 dengan cepat dan akurat, gunakan kalkulator atau tabel matematika. Alat-alat ini memberikan hasil yang tepat, terutama untuk bilangan besar atau kompleks.
Tip 2: Pahami sifat-sifat akar pangkat 2
Memahami sifat-sifat akar pangkat 2, seperti selalu menghasilkan bilangan positif untuk bilangan positif dan tidak terdefinisi untuk bilangan negatif, sangat penting untuk menghindari kesalahan dan memperoleh hasil yang bermakna.
Tip 3: Sederhanakan sebelum menghitung
Jika memungkinkan, sederhanakan ekspresi yang melibatkan akar pangkat 2 sebelum menghitung. Misalnya, faktorisasi bilangan di bawah akar pangkat 2 untuk menyederhanakan perhitungan.
Tip 4: Verifikasi hasil
Setelah menghitung akar pangkat 2, verifikasi hasil dengan mengkuadratkannya. Hasil kuadrat harus sama dengan bilangan aslinya, yang menunjukkan bahwa perhitungan tersebut benar.
Dengan mengikuti tips ini, Anda dapat menggunakan akar pangkat 2 secara efektif dan percaya diri untuk menyelesaikan masalah matematika dan fisika yang kompleks.
