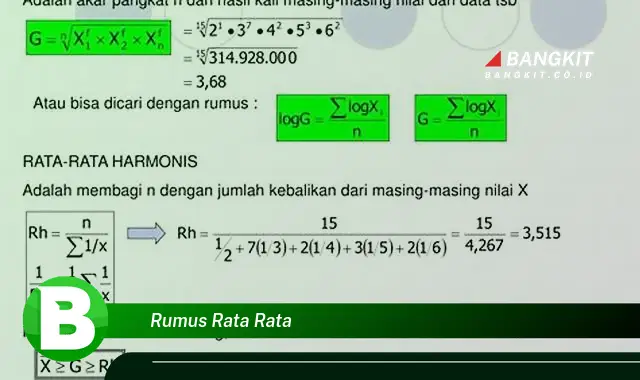
Rumus rata-rata adalah metode matematika yang digunakan untuk menentukan nilai rata-rata suatu kumpulan data. Nilai rata-rata ini dapat dihitung dengan menjumlahkan semua data dalam kumpulan data dan kemudian membaginya dengan jumlah data dalam kumpulan data. Rumus umum untuk menghitung rata-rata adalah:
Rata-rata = Jumlah semua data / Jumlah data
Contohnya, jika kita memiliki kumpulan data {2, 4, 6, 8, 10}, maka rata-ratanya adalah:
Rata-rata = (2 + 4 + 6 + 8 + 10) / 5 = 6
Rumus rata-rata sangat penting dalam berbagai bidang, seperti statistik, keuangan, dan sains. Rumus ini memungkinkan kita untuk meringkas kumpulan data yang besar menjadi satu nilai yang mewakili kecenderungan sentral dari data.
Rumus rata-rata pertama kali dikembangkan oleh matematikawan Persia abad ke-9, Al-Khwarizmi. Sejak saat itu, rumus ini telah menjadi alat penting dalam analisis data.
Pada artikel ini, kita akan membahas berbagai jenis rumus rata-rata, serta penggunaannya dalam berbagai bidang. Kita juga akan mengeksplorasi beberapa keterbatasan rumus rata-rata dan alternatifnya.
Rumus Rata-rata
Rumus rata-rata adalah metode penting untuk mengolah dan menganalisis data. Aspek-aspek esensial dari rumus rata-rata meliputi:
- Definisi
- Jenis
- Kegunaan
- Keterbatasan
- Alternatif
Rumus rata-rata didefinisikan sebagai metode matematis untuk menentukan nilai rata-rata suatu kumpulan data. Terdapat berbagai jenis rumus rata-rata, seperti rata-rata aritmatika, rata-rata geometrik, dan rata-rata harmonik. Masing-masing jenis rata-rata memiliki kegunaan spesifik dalam bidang yang berbeda.
Rumus rata-rata banyak digunakan dalam statistik, keuangan, dan sains. Rumus ini memungkinkan kita untuk meringkas kumpulan data yang besar menjadi satu nilai yang mewakili kecenderungan sentral dari data. Namun, rumus rata-rata juga memiliki keterbatasan, seperti sensitivitasnya terhadap nilai ekstrem.
Sebagai alternatif, terdapat beberapa metode lain untuk menghitung nilai rata-rata, seperti median dan modus. Masing-masing metode memiliki kelebihan dan kekurangannya sendiri, sehingga pemilihan metode yang tepat tergantung pada jenis data dan tujuan analisis.
Definisi
Definisi rumus rata-rata sangat penting karena memberikan dasar untuk memahami dan menggunakan rumus tersebut dengan benar. Definisi yang jelas dan ringkas menetapkan tujuan dan fungsi rumus, memungkinkan pengguna untuk menerapkannya secara efektif dalam berbagai situasi.
Rumus rata-rata didefinisikan sebagai metode matematis untuk menentukan nilai rata-rata suatu kumpulan data. Definisi ini menyoroti dua aspek utama rumus rata-rata: sifat matematisnya dan tujuannya untuk menghitung nilai rata-rata.
Memahami definisi rumus rata-rata sangat penting untuk menghindari kesalahan interpretasi dan penggunaan yang salah. Definisi yang tepat membantu pengguna untuk mengenali jenis data yang sesuai untuk rumus rata-rata, serta keterbatasan dan alternatifnya.
Jenis
Jenis rumus rata-rata sangat penting karena menentukan metode perhitungan nilai rata-rata yang sesuai untuk kumpulan data tertentu. Terdapat berbagai jenis rumus rata-rata, masing-masing dengan kelebihan dan kekurangannya sendiri.
Jenis rumus rata-rata yang umum digunakan meliputi:
- Rata-rata aritmatika
- Rata-rata geometrik
- Rata-rata harmonik
- Rata-rata tertimbang
- Rata-rata bergerak
Pemilihan jenis rumus rata-rata yang tepat bergantung pada jenis data yang akan dianalisis dan tujuan perhitungan. Misalnya, rata-rata aritmatika cocok untuk data yang mengikuti distribusi normal, sedangkan rata-rata harmonik cocok untuk data yang memiliki nilai nol.
Memahami jenis-jenis rumus rata-rata dan penggunaannya sangat penting untuk memastikan hasil perhitungan yang akurat dan bermakna. Pemilihan jenis rumus rata-rata yang tepat dapat membantu dalam pengambilan keputusan yang efektif dan pemahaman yang lebih baik terhadap data.
Kegunaan
Rumus rata-rata memiliki kegunaan yang luas dalam berbagai bidang, termasuk statistik, keuangan, dan sains. Kegunaan utama rumus rata-rata adalah untuk meringkas kumpulan data yang besar menjadi satu nilai yang mewakili kecenderungan sentral dari data. Nilai rata-rata ini dapat digunakan untuk membandingkan kumpulan data yang berbeda, mengidentifikasi tren, dan membuat prediksi.
Contohnya, dalam statistik, rumus rata-rata digunakan untuk menghitung nilai rata-rata suatu populasi berdasarkan sampel data. Nilai rata-rata ini dapat digunakan untuk membuat inferensi tentang populasi secara keseluruhan. Dalam keuangan, rumus rata-rata digunakan untuk menghitung nilai rata-rata return investasi. Nilai rata-rata ini dapat digunakan untuk mengevaluasi kinerja investasi dan membuat keputusan investasi yang lebih baik.
Memahami kegunaan rumus rata-rata sangat penting untuk memanfaatkannya secara efektif. Dengan memahami kegunaan rumus rata-rata, kita dapat menggunakannya untuk memperoleh wawasan berharga dari data dan membuat keputusan yang lebih baik.
Keterbatasan
Rumus rata-rata merupakan alat yang ampuh untuk meringkas data, namun memiliki keterbatasan tertentu yang perlu dipahami untuk menggunakannya secara efektif. Keterbatasan utama rumus rata-rata meliputi:
-
Sensitivitas terhadap nilai ekstrem
Rumus rata-rata sangat sensitif terhadap nilai ekstrem, baik nilai yang sangat tinggi maupun sangat rendah. Nilai ekstrem dapat mendistorsi nilai rata-rata, sehingga tidak lagi mewakili kecenderungan sentral data secara akurat.
-
Tidak memperhitungkan distribusi data
Rumus rata-rata tidak memperhitungkan distribusi data. Artinya, rumus rata-rata tidak dapat membedakan antara data yang terdistribusi secara normal dan data yang terdistribusi secara tidak normal. Hal ini dapat menyebabkan nilai rata-rata yang menyesatkan.
-
Tidak memberikan informasi tentang penyebaran data
Rumus rata-rata hanya memberikan informasi tentang nilai rata-rata data, tetapi tidak memberikan informasi tentang penyebaran data. Artinya, rumus rata-rata tidak dapat menunjukkan seberapa besar variasi data.
Memahami keterbatasan rumus rata-rata sangat penting untuk menggunakannya secara tepat dan menafsirkan hasilnya dengan benar. Dengan menyadari keterbatasan ini, kita dapat menggunakan rumus rata-rata secara efektif untuk mendapatkan wawasan berharga dari data.
Alternatif
Dalam konteks rumus rata-rata, alternatif mengacu pada metode perhitungan lain yang dapat digunakan untuk mengukur kecenderungan sentral suatu kumpulan data. Meskipun rumus rata-rata banyak digunakan, terdapat beberapa alternatif yang dapat mengatasi keterbatasannya.
-
Median
Median adalah nilai tengah suatu kumpulan data ketika data diurutkan dari nilai terkecil ke terbesar. Median tidak terpengaruh oleh nilai ekstrem, sehingga menjadi alternatif yang lebih robust terhadap rumus rata-rata ketika terdapat data pencilan. -
Modus
Modus adalah nilai yang paling sering muncul dalam suatu kumpulan data. Modus memberikan informasi tentang nilai yang paling representatif dalam suatu kumpulan data, tetapi tidak selalu menjadi ukuran kecenderungan sentral yang baik ketika terdapat beberapa nilai yang muncul sama sering. -
Rata-rata terpotong
Rata-rata terpotong dihitung dengan membuang persentase tertentu dari nilai ekstrem teratas dan terbawah suatu kumpulan data, kemudian menghitung rata-rata dari nilai yang tersisa. Metode ini mengurangi pengaruh nilai ekstrem pada nilai rata-rata. -
Rata-rata winsorized
Rata-rata winsorized mirip dengan rata-rata terpotong, tetapi nilai ekstrem tidak dibuang melainkan diganti dengan nilai persentil tertentu. Metode ini juga mengurangi pengaruh nilai ekstrem pada nilai rata-rata.
Pilihan alternatif rumus rata-rata yang tepat bergantung pada sifat data, tujuan analisis, dan tingkat sensitivitas terhadap nilai ekstrem yang dapat diterima. Dengan memahami alternatif yang tersedia, pengguna dapat memilih metode yang paling sesuai untuk kebutuhan spesifik mereka.
FAQ tentang Rumus Rata-rata
Bagian ini menyajikan beberapa pertanyaan umum dan jawabannya terkait rumus rata-rata untuk memberikan pemahaman yang lebih komprehensif.
Pertanyaan 1: Apa itu rumus rata-rata dan bagaimana cara menghitungnya?
Rumus rata-rata adalah metode matematika untuk menentukan nilai rata-rata suatu kumpulan data. Rumus umum untuk menghitung rata-rata adalah menjumlahkan semua data dalam kumpulan data dan membaginya dengan jumlah data dalam kumpulan data.
Pertanyaan 2: Apa saja jenis-jenis rumus rata-rata?
Terdapat beberapa jenis rumus rata-rata, di antaranya rata-rata aritmatika, rata-rata geometrik, rata-rata harmonik, rata-rata tertimbang, dan rata-rata bergerak. Masing-masing jenis rata-rata memiliki kegunaan spesifik dalam bidang yang berbeda.
Pertanyaan 3: Apa saja keterbatasan rumus rata-rata?
Rumus rata-rata memiliki beberapa keterbatasan, seperti sensitivitasnya terhadap nilai ekstrem, tidak memperhitungkan distribusi data, dan tidak memberikan informasi tentang penyebaran data.
Pertanyaan 4: Apa saja alternatif rumus rata-rata?
Alternatif rumus rata-rata meliputi median, modus, rata-rata terpotong, dan rata-rata winsorized. Pemilihan alternatif yang tepat bergantung pada sifat data, tujuan analisis, dan tingkat sensitivitas terhadap nilai ekstrem yang dapat diterima.
Dengan memahami pertanyaan dan jawaban ini, Anda diharapkan dapat menggunakan rumus rata-rata secara efektif dan tepat.
Tips Tambahan:
– Selalu periksa jenis data sebelum memilih rumus rata-rata yang sesuai.
– Pertimbangkan keterbatasan rumus rata-rata dan pilih alternatif yang sesuai jika diperlukan.
– Interpretasikan hasil perhitungan rata-rata dengan hati-hati dan dalam konteks data yang dianalisis.
Tips Menggunakan Rumus Rata-Rata
Dalam menggunakan rumus rata-rata, terdapat beberapa tips yang perlu diperhatikan untuk memastikan hasil perhitungan yang akurat dan bermakna:
Tip 1: Tentukan Jenis Data
Sebelum menggunakan rumus rata-rata, penting untuk menentukan jenis data yang akan dianalisis. Berbeda jenis data memerlukan jenis rumus rata-rata yang berbeda pula. Misalnya, untuk data kontinu yang terdistribusi normal, digunakan rata-rata aritmatika. Sedangkan untuk data kategorikal, digunakan modus atau median.
Tip 2: Perhatikan Keterbatasan
Rumus rata-rata memiliki beberapa keterbatasan yang perlu dipahami. Salah satu keterbatasannya adalah sensitivitas terhadap nilai ekstrem. Nilai ekstrem dapat memengaruhi nilai rata-rata dan membuatnya tidak lagi mewakili kecenderungan sentral data. Dalam kasus ini, dapat digunakan alternatif seperti median atau rata-rata terpotong.
Tip 3: Pertimbangkan Distribusi Data
Rumus rata-rata tidak memperhitungkan distribusi data. Artinya, rumus rata-rata tidak dapat membedakan antara data yang terdistribusi normal dan data yang terdistribusi tidak normal. Hal ini dapat menyebabkan nilai rata-rata yang menyesatkan. Untuk data yang terdistribusi tidak normal, dapat digunakan alternatif seperti median atau modus.
Tip 4: Tafsirkan Hasil dengan Hati-hati
Hasil perhitungan rata-rata harus ditafsirkan dengan hati-hati dan dalam konteks data yang dianalisis. Nilai rata-rata hanya memberikan informasi tentang kecenderungan sentral data, tetapi tidak memberikan informasi tentang penyebaran data. Untuk mendapatkan gambaran yang lebih lengkap tentang data, perlu dipertimbangkan juga ukuran penyebaran seperti simpangan baku atau jangkauan.
Dengan mengikuti tips di atas, Anda dapat menggunakan rumus rata-rata secara efektif dan tepat untuk mendapatkan wawasan berharga dari data yang dianalisis.
