Intip Rahasia Luas Permukaan Kubus yang Bikin Kamu Penasaran

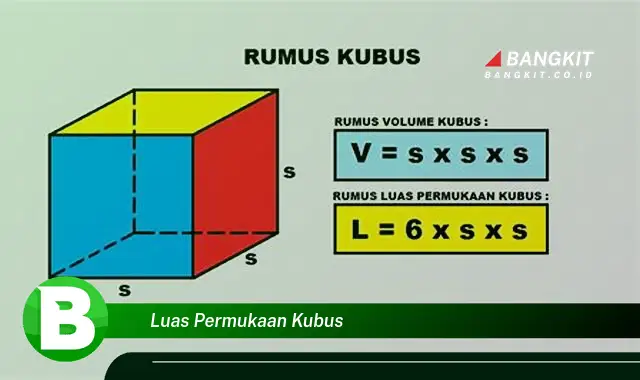
Luas permukaan kubus adalah jumlah luas semua sisi kubus. Kubus memiliki enam sisi yang berbentuk persegi, sehingga luas permukaan kubus dapat dihitung dengan mengalikan luas salah satu sisinya dengan enam. Rumus untuk menghitung luas permukaan kubus adalah 6 x s, dimana s adalah panjang sisi kubus.

Luas permukaan kubus sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Dalam arsitektur, luas permukaan kubus digunakan untuk menghitung luas permukaan bangunan dan menentukan kebutuhan bahan bangunan. Dalam teknik, luas permukaan kubus digunakan untuk menghitung luas permukaan benda-benda tiga dimensi, seperti balok dan prisma. Dalam desain, luas permukaan kubus digunakan untuk menentukan luas permukaan benda-benda dekoratif, seperti vas dan lampu.

Konsep luas permukaan kubus telah dikenal sejak zaman kuno. Bangsa Mesir kuno menggunakan konsep ini untuk membangun piramida, dan bangsa Yunani kuno menggunakannya untuk menghitung volume kubus. Pada abad ke-17, matematikawan Ren Descartes mengembangkan rumus untuk menghitung luas permukaan kubus, yang masih digunakan hingga saat ini.

Luas Permukaan Kubus

Luas permukaan kubus merupakan aspek penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain. Berikut adalah lima aspek penting terkait luas permukaan kubus:

• Rumus: 6 x s²
• Satuan: Satuan luas, seperti cm² atau m²
• Sifat: Berbanding lurus dengan kuadrat panjang sisi
• Aplikasi: Menghitung luas permukaan bangunan, benda tiga dimensi, dan benda dekoratif
• Sejarah: Dikenal sejak zaman kuno, digunakan dalam pembangunan piramida dan perhitungan volume kubus

Kelima aspek tersebut saling berkaitan dan membentuk pemahaman yang komprehensif tentang luas permukaan kubus. Rumus yang digunakan untuk menghitung luas permukaan kubus sangat penting karena menjadi dasar perhitungan dalam berbagai aplikasi. Satuan yang digunakan harus sesuai dengan konteks penggunaan, sehingga hasil perhitungan dapat diinterpretasikan dengan tepat. Sifat luas permukaan kubus yang berbanding lurus dengan kuadrat panjang sisi menunjukkan bahwa semakin besar panjang sisi kubus, semakin besar pula luas permukaannya. Berbagai aplikasi luas permukaan kubus dalam bidang arsitektur, teknik, dan desain menunjukkan pentingnya konsep ini dalam kehidupan nyata. Terakhir, sejarah luas permukaan kubus yang telah dikenal sejak zaman kuno hingga saat ini menunjukkan bahwa konsep ini memiliki nilai yang bertahan lama dan terus digunakan hingga sekarang.

Rumus

Rumus 6 x s² merupakan rumus untuk menghitung luas permukaan kubus, di mana s adalah panjang sisi kubus. Rumus ini sangat penting karena menjadi dasar perhitungan luas permukaan kubus dalam berbagai aplikasi.

• Menghitung Luas Permukaan Kubus: Rumus ini digunakan untuk menghitung luas permukaan kubus dengan mengalikan panjang sisi kubus dengan 6. Misalnya, jika panjang sisi kubus adalah 5 cm, maka luas permukaan kubus adalah 6 x 5² = 150 cm².
• Sifat Luas Permukaan Kubus: Rumus ini menunjukkan bahwa luas permukaan kubus berbanding lurus dengan kuadrat panjang sisi kubus. Artinya, jika panjang sisi kubus diperbesar dua kali, maka luas permukaan kubus akan menjadi empat kali lebih besar.
• Aplikasi dalam Arsitektur: Rumus ini digunakan dalam arsitektur untuk menghitung luas permukaan bangunan yang berbentuk kubus atau balok. Luas permukaan bangunan tersebut digunakan untuk menentukan kebutuhan bahan bangunan dan memperkirakan biaya pembangunan.
• Aplikasi dalam Teknik: Rumus ini digunakan dalam teknik untuk menghitung luas permukaan benda-benda tiga dimensi yang berbentuk kubus atau balok. Luas permukaan benda-benda tersebut digunakan untuk menentukan gaya yang bekerja pada benda dan merancang struktur yang aman dan efisien.

Dengan memahami rumus 6 x s², kita dapat menghitung luas permukaan kubus dengan mudah dan akurat. Rumus ini memiliki aplikasi yang luas dalam berbagai bidang, sehingga menjadi konsep penting dalam matematika dan sains.

Satuan

Satuan luas, seperti cm² atau m², merupakan komponen penting dalam konsep luas permukaan kubus. Satuan luas digunakan untuk menyatakan besaran luas permukaan kubus dan memastikan bahwa hasil perhitungan dapat diinterpretasikan dengan tepat.

Luas permukaan kubus dinyatakan dalam satuan luas karena merupakan ukuran luas daerah permukaan kubus. Satuan luas yang digunakan harus sesuai dengan konteks penggunaan. Misalnya, jika luas permukaan kubus diukur dalam sentimeter, maka satuan luas yang digunakan adalah cm². Sementara itu, jika luas permukaan kubus diukur dalam meter, maka satuan luas yang digunakan adalah m².

Penggunaan satuan luas yang tepat sangat penting untuk menghindari kesalahan interpretasi hasil perhitungan. Misalnya, jika luas permukaan kubus dinyatakan dalam cm², tetapi ditafsirkan sebagai m², maka hasil perhitungan akan menjadi 100 kali lebih kecil dari nilai sebenarnya. Oleh karena itu, memahami satuan luas yang digunakan dalam perhitungan luas permukaan kubus sangat penting untuk memastikan akurasi dan keandalan hasil.

Sifat

Sifat luas permukaan kubus yang berbanding lurus dengan kuadrat panjang sisi merupakan aspek penting dalam memahami dan mengaplikasikan konsep luas permukaan kubus. Sifat ini menunjukkan keterkaitan antara panjang sisi kubus dan luas permukaannya, yang memiliki implikasi yang luas dalam berbagai bidang. Berikut adalah penjelasan lebih detail mengenai sifat ini:

• Pengaruh Panjang Sisi: Panjang sisi kubus memiliki pengaruh yang signifikan terhadap luas permukaannya. Jika panjang sisi kubus diperbesar, maka luas permukaannya akan meningkat secara proporsional. Misalnya, jika panjang sisi kubus diperbesar dua kali, maka luas permukaannya akan menjadi empat kali lebih besar.
• Aplikasi dalam Desain: Sifat ini penting dalam desain dan konstruksi, terutama saat menentukan luas permukaan bangunan atau benda tiga dimensi lainnya. Dengan memahami hubungan antara panjang sisi dan luas permukaan, desainer dan insinyur dapat mengoptimalkan penggunaan ruang dan bahan secara efisien.
• Implikasi Matematika: Sifat ini memiliki implikasi matematis yang penting. Misalnya, dalam persamaan luas permukaan kubus (6 x s²), nilai 6 merupakan konstanta yang menunjukkan hubungan proporsional antara luas permukaan dan kuadrat panjang sisi.
• Pemahaman Konseptual: Memahami sifat ini membantu dalam membangun pemahaman konseptual yang kuat tentang luas permukaan kubus. Sifat ini menunjukkan bahwa luas permukaan kubus tidak hanya bergantung pada satu dimensi (panjang sisi), tetapi juga pada dimensi kuadrat (kuadrat panjang sisi).

Dengan memahami sifat luas permukaan kubus yang berbanding lurus dengan kuadrat panjang sisi, kita dapat lebih memahami, mengaplikasikan, dan mengoptimalkan konsep luas permukaan kubus dalam berbagai bidang.

Aplikasi

Konsep luas permukaan kubus memiliki aplikasi yang luas dalam kehidupan sehari-hari, terutama dalam menghitung luas permukaan berbagai objek, seperti bangunan, benda tiga dimensi, dan benda dekoratif. Aplikasi-aplikasi ini sangat penting dalam berbagai bidang, seperti arsitektur, teknik, dan desain.

• Bangunan: Luas permukaan kubus digunakan untuk menghitung luas permukaan bangunan yang berbentuk kubus atau balok. Mengetahui luas permukaan bangunan sangat penting untuk menentukan kebutuhan bahan bangunan, memperkirakan biaya pembangunan, dan merencanakan tata letak interior.
• Benda Tiga Dimensi: Luas permukaan kubus juga digunakan untuk menghitung luas permukaan benda-benda tiga dimensi lainnya, seperti balok, prisma, dan limas. Mengetahui luas permukaan benda-benda ini penting dalam bidang teknik, seperti dalam perhitungan gaya yang bekerja pada benda dan desain struktur yang aman dan efisien.
• Benda Dekoratif: Luas permukaan kubus juga digunakan dalam desain benda-benda dekoratif, seperti vas, lampu, dan patung. Mengetahui luas permukaan benda-benda dekoratif penting untuk menentukan kebutuhan bahan, memperkirakan biaya produksi, dan mengoptimalkan estetika.

Dengan memahami aplikasi luas permukaan kubus dalam berbagai bidang, kita dapat mengapresiasi pentingnya konsep ini dalam kehidupan sehari-hari. Konsep ini tidak hanya terbatas pada bidang matematika, tetapi juga memiliki implikasi yang luas dalam bidang arsitektur, teknik, dan desain.

Sejarah

Sejarah penggunaan luas permukaan kubus dapat ditelusuri hingga zaman kuno, di mana konsep ini telah digunakan dalam pembangunan piramida dan perhitungan volume kubus. Hal ini menunjukkan pemahaman mendalam tentang geometri dan matematika yang dimiliki oleh peradaban kuno.

• Pembangunan Piramida

  Bangsa Mesir kuno menggunakan konsep luas permukaan kubus dalam pembangunan piramida. Mereka memahami bahwa luas permukaan piramida dapat dihitung dengan menjumlahkan luas permukaan semua sisi segitiga yang membentuk piramida. Pemahaman ini memungkinkan mereka membangun piramida dengan ukuran dan bentuk yang presisi.

• Perhitungan Volume Kubus

  Bangsa Yunani kuno menggunakan konsep luas permukaan kubus untuk menghitung volume kubus. Mereka membuktikan bahwa volume kubus sama dengan luas permukaan kubus dikalikan dengan sepertiga dari panjang sisinya. Teorema ini dikenal sebagai Teorema Kubus, yang merupakan dasar untuk menghitung volume benda-benda tiga dimensi lainnya.

Dengan memahami sejarah penggunaan luas permukaan kubus, kita dapat mengapresiasi pentingnya konsep ini dalam perkembangan matematika dan peradaban manusia. Konsep ini telah digunakan selama berabad-abad untuk menyelesaikan masalah praktis dan memajukan pemahaman kita tentang dunia di sekitar kita.

Pertanyaan Umum tentang Luas Permukaan Kubus

Berikut adalah beberapa pertanyaan umum tentang luas permukaan kubus beserta jawabannya untuk memberikan pemahaman yang lebih baik tentang konsep ini.

Pertanyaan 1: Bagaimana cara menghitung luas permukaan kubus?

Jawaban: Luas permukaan kubus dihitung dengan mengalikan luas salah satu sisinya dengan 6. Rumus untuk menghitung luas permukaan kubus adalah 6 x s², di mana s adalah panjang sisi kubus.

Pertanyaan 2: Apa saja aplikasi luas permukaan kubus dalam kehidupan nyata?

Jawaban: Luas permukaan kubus memiliki banyak aplikasi dalam kehidupan nyata, seperti menghitung luas permukaan bangunan, benda tiga dimensi, dan benda dekoratif. Konsep ini juga digunakan dalam arsitektur, teknik, dan desain.

Pertanyaan 3: Mengapa luas permukaan kubus berbanding lurus dengan kuadrat panjang sisi?

Jawaban: Karena luas permukaan kubus dihitung dengan mengalikan luas salah satu sisinya dengan 6, maka luas permukaan kubus akan berbanding lurus dengan kuadrat panjang sisi. Jika panjang sisi kubus diperbesar dua kali, maka luas permukaan kubus akan menjadi empat kali lebih besar.

Pertanyaan 4: Apa saja satuan yang digunakan untuk menyatakan luas permukaan kubus?

Jawaban: Luas permukaan kubus dinyatakan dalam satuan luas, seperti sentimeter persegi (cm²) atau meter persegi (m²). Satuan yang digunakan harus sesuai dengan konteks penggunaan.

Dengan memahami jawaban atas pertanyaan umum ini, diharapkan dapat memberikan pemahaman yang lebih baik tentang konsep luas permukaan kubus dan aplikasinya dalam berbagai bidang.

Tips: Untuk mempelajari lebih lanjut tentang luas permukaan kubus, disarankan untuk membaca artikel lanjutan tentang topik ini atau berkonsultasi dengan sumber terpercaya lainnya.

Tips Mempelajari Luas Permukaan Kubus

Berikut adalah beberapa tips untuk mempelajari luas permukaan kubus secara efektif:

Tip 1: Pahami Konsep Dasar
Mulailah dengan memahami konsep dasar luas permukaan kubus, yaitu jumlah luas semua sisinya. Bayangkan kubus sebagai sebuah kotak yang memiliki enam sisi persegi. Luas permukaan kubus dihitung dengan mengalikan luas salah satu sisinya dengan 6.

Tip 2: Gunakan Rumus yang Tepat
Hafalkan rumus untuk menghitung luas permukaan kubus, yaitu 6 x s², di mana s adalah panjang sisi kubus. Rumus ini sangat penting karena menjadi dasar perhitungan luas permukaan kubus dalam berbagai aplikasi.

Tip 3: Latih Soal-Soal
Untuk menguasai konsep luas permukaan kubus, latihan soal sangat penting. Carilah soal-soal latihan dari berbagai sumber, seperti buku teks, latihan online, atau soal-soal ujian. Dengan berlatih soal, Anda dapat menguji pemahaman Anda dan meningkatkan keterampilan menghitung luas permukaan kubus.

Tip 4: Terapkan dalam Konteks Nyata
Cobalah untuk menerapkan konsep luas permukaan kubus dalam konteks nyata. Misalnya, hitunglah luas permukaan kubus yang mewakili sebuah ruangan atau luas permukaan sebuah dadu. Dengan menerapkan konsep ini dalam situasi nyata, Anda dapat memahami kegunaan dan pentingnya luas permukaan kubus dalam kehidupan sehari-hari.

Dengan mengikuti tips-tips di atas, Anda dapat mempelajari luas permukaan kubus secara efektif dan memahami konsep serta aplikasinya dengan baik.