FPB (Faktor Persekutuan Terbesar) dan KPK (Kelipatan Persekutuan Terkecil) merupakan dua konsep penting dalam matematika, khususnya teori bilangan. FPB adalah faktor terbesar yang membagi dua atau lebih bilangan bulat positif, sedangkan KPK adalah kelipatan terkecil yang habis dibagi oleh dua atau lebih bilangan bulat positif.
FPB dan KPK memiliki banyak aplikasi dalam kehidupan sehari-hari, seperti pada masalah pembagian, pengukuran, dan geometri. Selain itu, konsep FPB dan KPK juga memiliki peran penting dalam perkembangan matematika, seperti pada bidang aljabar dan analisis bilangan.
Pada artikel ini, kita akan membahas secara mendalam tentang FPB dan KPK, termasuk definisi, sifat-sifat, cara menghitung, dan aplikasinya dalam berbagai bidang.
FPB dan KPK
FPB dan KPK merupakan konsep dasar dalam matematika yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Berikut lima aspek penting yang terkait dengan FPB dan KPK:
- Definisi
- Sifat-sifat
- Cara menghitung
- Aplikasi
- Sejarah
FPB dan KPK memiliki hubungan yang erat. FPB digunakan untuk mencari faktor-faktor persekutuan dari dua atau lebih bilangan, sedangkan KPK digunakan untuk mencari kelipatan persekutuan dari dua atau lebih bilangan. Kedua konsep ini juga digunakan dalam penyederhanaan pecahan dan perbandingan bilangan.
Selain itu, FPB dan KPK juga memiliki aplikasi luas dalam bidang-bidang seperti aljabar, geometri, dan teori bilangan. Misalnya, FPB digunakan untuk mencari penyelesaian sistem persamaan linear, sedangkan KPK digunakan untuk mencari kelipatan persekutuan terkecil dari dua atau lebih polinomial.
Definisi
Definisi FPB dan KPK sangat penting dalam memahami kedua konsep ini. FPB adalah faktor terbesar yang membagi dua atau lebih bilangan bulat positif, sedangkan KPK adalah kelipatan terkecil yang habis dibagi oleh dua atau lebih bilangan bulat positif.
Definisi FPB dan KPK ini memiliki implikasi yang luas dalam matematika. Misalnya, definisi FPB digunakan untuk mencari faktor-faktor persekutuan dari dua atau lebih bilangan, sedangkan definisi KPK digunakan untuk mencari kelipatan persekutuan dari dua atau lebih bilangan. Kedua konsep ini juga digunakan dalam penyederhanaan pecahan dan perbandingan bilangan.
Selain itu, definisi FPB dan KPK juga memiliki aplikasi luas dalam bidang-bidang seperti aljabar, geometri, dan teori bilangan. Misalnya, FPB digunakan untuk mencari penyelesaian sistem persamaan linear, sedangkan KPK digunakan untuk mencari kelipatan persekutuan terkecil dari dua atau lebih polinomial.
Sifat-sifat
Sifat-sifat FPB dan KPK sangat penting dalam memahami dan mengaplikasikan konsep-konsep ini dalam berbagai bidang matematika. Berikut lima sifat utama FPB dan KPK:
-
Sifat Asosiatif
Sifat asosiatif menyatakan bahwa FPB dan KPK dari tiga bilangan atau lebih dapat dihitung dengan mengelompokkannya secara sembarang. Misalnya, FPB(a, b, c) = FPB(FPB(a, b), c) dan KPK(a, b, c) = KPK(KPK(a, b), c). -
Sifat Komutatif
Sifat komutatif menyatakan bahwa urutan bilangan dalam menghitung FPB dan KPK tidak mempengaruhi hasilnya. Misalnya, FPB(a, b) = FPB(b, a) dan KPK(a, b) = KPK(b, a). -
Sifat Distributif
Sifat distributif menyatakan bahwa FPB dan KPK dari beberapa bilangan yang merupakan faktor atau kelipatan dari bilangan lain dapat dihitung dengan mengalikan atau membagi bilangan-bilangan tersebut. Misalnya, FPB(a b, c) = FPB(a, c) FPB(b, c) dan KPK(a b, c) = KPK(a, c) KPK(b, c). -
Sifat Identitas
Sifat identitas menyatakan bahwa FPB dari suatu bilangan dengan 1 adalah bilangan itu sendiri, dan KPK dari suatu bilangan dengan 1 adalah bilangan itu sendiri. Misalnya, FPB(a, 1) = a dan KPK(a, 1) = a. -
Sifat Sifat Monoton
Sifat monoton menyatakan bahwa jika suatu bilangan ditambahkan atau dikurangi dengan bilangan lain, maka FPB dan KPK dari bilangan-bilangan tersebut akan berubah. Misalnya, jika a > b, maka FPB(a + b, b) < FPB(a, b) dan KPK(a + b, b) > KPK(a, b).
Sifat-sifat ini sangat berguna dalam berbagai aplikasi FPB dan KPK. Misalnya, sifat asosiatif memudahkan kita menghitung FPB dan KPK dari tiga bilangan atau lebih dengan mengelompokkannya secara efisien. Sifat komutatif memungkinkan kita menghitung FPB dan KPK dalam urutan bilangan yang sesuai. Sifat distributif memudahkan kita menghitung FPB dan KPK dari bilangan-bilangan yang merupakan faktor atau kelipatan dari bilangan lain. Sifat identitas menunjukkan bahwa 1 merupakan faktor dan kelipatan dari semua bilangan. Sifat monoton menunjukkan bagaimana FPB dan KPK berubah ketika bilangan-bilangan diubah.
Cara Menghitung FPB dan KPK
Mengetahui cara menghitung FPB dan KPK sangat penting untuk memahami dan mengaplikasikan konsep-konsep ini. Ada beberapa metode untuk menghitung FPB dan KPK, antara lain:
-
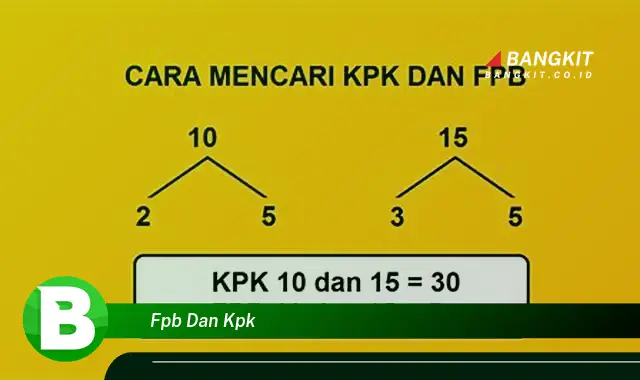
Metode Faktorisasi Prima
Metode faktorisasi prima melibatkan penguraian bilangan-bilangan yang diberikan menjadi faktor-faktor primanya. FPB adalah perkalian faktor-faktor prima yang sama, sedangkan KPK adalah perkalian semua faktor prima yang terlibat. -
Metode Euclidean
Metode Euclidean adalah algoritma berulang yang digunakan untuk menghitung FPB dari dua bilangan. Algoritma ini dimulai dengan membagi bilangan yang lebih besar dengan bilangan yang lebih kecil, kemudian membagi sisa dengan bilangan yang lebih kecil, dan seterusnya. FPB adalah sisa terakhir yang diperoleh. -
Metode Pengurangan Berulang
Metode pengurangan berulang melibatkan pengurangan bilangan yang lebih kecil dari bilangan yang lebih besar secara berulang-ulang hingga kedua bilangan menjadi sama. Bilangan yang sama tersebut adalah FPB dari kedua bilangan awal.
Cara menghitung FPB dan KPK sangat penting dalam berbagai aplikasi matematika. Misalnya, FPB digunakan untuk mencari penyelesaian sistem persamaan linear, sedangkan KPK digunakan untuk mencari kelipatan persekutuan terkecil dari dua atau lebih polinomial.
Aplikasi
FPB dan KPK memiliki banyak aplikasi dalam kehidupan sehari-hari, mulai dari bidang matematika dasar hingga bidang yang lebih kompleks seperti fisika dan teknik. Berikut beberapa aplikasi penting FPB dan KPK:
-
Matematika dasar
FPB dan KPK digunakan dalam berbagai operasi matematika dasar, seperti penyederhanaan pecahan, perbandingan bilangan, dan penyelesaian sistem persamaan linear. -
Geometri
FPB dan KPK digunakan dalam berbagai masalah geometri, seperti mencari panjang sisi segitiga siku-siku atau mencari luas persegi panjang yang sebangun. -
Fisika
FPB dan KPK digunakan dalam berbagai masalah fisika, seperti mencari frekuensi resonansi atau mencari kecepatan benda yang bergerak melingkar. -
Teknik
FPB dan KPK digunakan dalam berbagai masalah teknik, seperti mencari faktor keamanan suatu struktur atau mencari periode getaran suatu sistem mekanik.
Aplikasi FPB dan KPK sangat luas dan beragam. Konsep-konsep ini merupakan dasar dari banyak bidang matematika dan sains, dan memiliki peran penting dalam memecahkan masalah dunia nyata.
Sejarah
Konsep FPB dan KPK telah dikenal sejak zaman kuno. Para ahli matematika pada masa itu, seperti Euclid dan Archimedes, telah menggunakan konsep-konsep ini dalam karya-karya mereka. Seiring perkembangan matematika, FPB dan KPK menjadi konsep dasar yang penting dalam berbagai bidang matematika, seperti teori bilangan, aljabar, dan geometri.
Pada zaman modern, FPB dan KPK masih memainkan peran penting dalam berbagai aplikasi matematika dan sains. Misalnya, FPB digunakan dalam kriptografi untuk mencari kunci enkripsi dan dekripsi yang aman. KPK digunakan dalam fisika untuk mencari frekuensi resonansi suatu sistem mekanik. Selain itu, FPB dan KPK juga digunakan dalam berbagai aplikasi komputer, seperti pencarian algoritma yang efisien dan optimalisasi kinerja sistem.
Memahami sejarah FPB dan KPK sangat penting untuk memahami perkembangan matematika dan aplikasinya dalam berbagai bidang. Sejarah ini menunjukkan bahwa konsep-konsep dasar matematika, seperti FPB dan KPK, memiliki nilai yang abadi dan terus digunakan untuk memecahkan masalah dunia nyata.
Pertanyaan Umum tentang FPB dan KPK
Berikut beberapa pertanyaan umum tentang FPB dan KPK, beserta jawabannya:
Pertanyaan 1: Apa itu FPB dan KPK?
FPB (Faktor Persekutuan Terbesar) adalah faktor terbesar yang membagi habis dua atau lebih bilangan bulat positif. KPK (Kelipatan Persekutuan Terkecil) adalah kelipatan terkecil yang habis dibagi oleh dua atau lebih bilangan bulat positif.
Pertanyaan 2: Bagaimana cara menghitung FPB dan KPK?
Ada beberapa metode untuk menghitung FPB dan KPK, di antaranya metode faktorisasi prima, metode Euclidean, dan metode pengurangan berulang.
Pertanyaan 3: Apa saja aplikasi FPB dan KPK?
FPB dan KPK memiliki banyak aplikasi dalam matematika dan sains, seperti dalam penyederhanaan pecahan, perbandingan bilangan, geometri, fisika, dan teknik.
Pertanyaan 4: Mengapa FPB dan KPK penting dalam matematika?
FPB dan KPK merupakan konsep dasar yang penting dalam berbagai bidang matematika, seperti teori bilangan, aljabar, dan geometri. Kedua konsep ini digunakan dalam penyelesaian berbagai masalah matematika.
Kesimpulan
FPB dan KPK adalah konsep penting dalam matematika yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Memahami konsep-konsep ini sangat penting untuk menyelesaikan berbagai masalah matematika dan sains.
Tips
Untuk memperdalam pemahaman Anda tentang FPB dan KPK, Anda dapat membaca buku-buku atau artikel tentang topik ini, mengikuti kursus online, atau berlatih soal-soal latihan.
Tips Memahami FPB dan KPK
Untuk memperdalam pemahaman Anda tentang FPB dan KPK, Anda dapat mengikuti tips berikut:
Tip 1: Pahami Konsep Dasar
Sebelum mempelajari FPB dan KPK lebih lanjut, pastikan Anda memahami konsep dasar matematika seperti faktor, kelipatan, dan bilangan prima.
Tip 2: Kuasai Metode Perhitungan
Ada beberapa metode untuk menghitung FPB dan KPK, seperti metode faktorisasi prima, algoritma Euclidean, dan metode pengurangan berulang. Kuasailah metode-metode ini agar Anda dapat menghitung FPB dan KPK dengan cepat dan tepat.
Tip 3: Latih Soal Secara Teratur
Cara terbaik untuk meningkatkan pemahaman Anda tentang FPB dan KPK adalah dengan berlatih soal secara teratur. Carilah soal-soal latihan dari berbagai sumber, seperti buku teks, soal ujian, atau situs web.
Tip 4: Terapkan dalam Masalah Dunia Nyata
FPB dan KPK memiliki banyak aplikasi dalam kehidupan sehari-hari. Cobalah untuk menerapkan konsep-konsep ini dalam masalah dunia nyata, seperti mencari faktor persekutuan terbesar dari dua atau lebih bilangan yang mewakili panjang, atau mencari kelipatan persekutuan terkecil dari dua atau lebih bilangan yang mewakili waktu.
